El 28 de octubre publicamos el desafío ESET #43 en el que los participantes debían encontrar el flag tras descubrir la clave privavda y descifrar el mensaje oculto. Además de presentar la solución al desafío, anunciamos el nombre del único ganador, quien ha ganado una licencia de ESET Mobile Security para Android y la posibilidad de realizar uno de los cursos disponibles en nuestra plataforma Academia ESET.
El único ganador de este desafío fue:
- Jere Pretto
El ganador deberá comunicarse por mensaje privado a través de alguna de nuestras redes sociales, como Facebook, Twitter o Instagram, indicando su nombre y dirección de correo para que podamos hacer entrega del premio. Desde ya, agradecemos a todos los que participaron y dedicaron parte de su tiempo a intentar resolver el desafío.
A continuación, presentamos la solución al desafío.
Resolución del desafío #43
En el desafío mencionamos que se dispone de un mensaje que fue cifrado utilizando la clave pública de algún miembro de Evil Corp. Es evidente que para resolver este desafío, vamos a necesitar obtener la clave privada de algún miembro de la organización basándonos solamente en sus claves públicas. Esto significa que debe existir alguna vulnerabilidad en alguno de los certificados en la lista.
Primero, repasemos muy brevemente cómo se cifra y descifra un mensaje utilizando RSA:
- cifrado con la clave pública
C = M^e mod n
donde: n ≡ p * q
- descifrado con la clave privada
M = C^d mod n
donde: d ≡ e^−1 mod (mcm(p − 1, q − 1))
El número n es público y se calcula como la multiplicación de dos números primos que tienen que ser aleatorios, y está presente tanto en la clave pública como en la privada. Mientras que el número e es fácil de obtener, ya que siempre se suelen utilizar los mismos valores y en el enunciado del desafío se aclara que su valor es estándar.
Si queremos descifrar el mensaje, debemos conocer los valores individuales de p y q para poder calcular el último componente de la ecuación, el exponente privado, d.
e * dₚ = d mod ( p - 1 )
e * dᵩ = d mod ( q - 1 )
Si p y q son números lo suficientemente grandes y verdaderamente aleatorios, calcular estos valores sería una tarea imposible. Sin embargo, la implementación tiene una serie de errores. Lo más crítico es que las claves fueron generadas con un esquema que no es lo suficientemente aleatorio, de tal forma que al menos dos de las claves públicas fueron generadas con un factor primo en común.
¿Qué ocurre cuando dos claves públicas distintas utilizan el mismo valor de p o el mismo valor de q? En ese caso, podríamos averiguar el Máximo Común Divisor (MCD) de ambas utilizando el Algoritmo de Euclides. Para esto, existen herramientas de código abierto que nos permiten realizar este cálculo de forma sencilla.
Si logramos obtener cualquiera de estos dos valores, calcular el último es trivial, ya que:
q = n / p ; p = n / q
Probemos aplicar el algoritmo de Euclides a todas las claves en la lista de claves públicas.

Fig 1. Claves públicas con factores primos en común
Efectivamente, encontramos un par de claves que tienen un MCD en común. Recordemos que los valores p y q son primos, por lo tanto siempre tienen un MCD = 1, pero si encontramos un valor más alto, significa que fueron generados en un sistema de baja entropía y comparten al menos uno de los dos factores.
Con esta información ya podemos calcular el valor del exponente privado d y generar la clave privada. Primero, debemos asumir un valor para e, que típicamente es 65537 y en este ejercicio también lo es.
Veamos el siguiente código en Python, utilizando la librería pycrypto para reconstruir la clave privada:
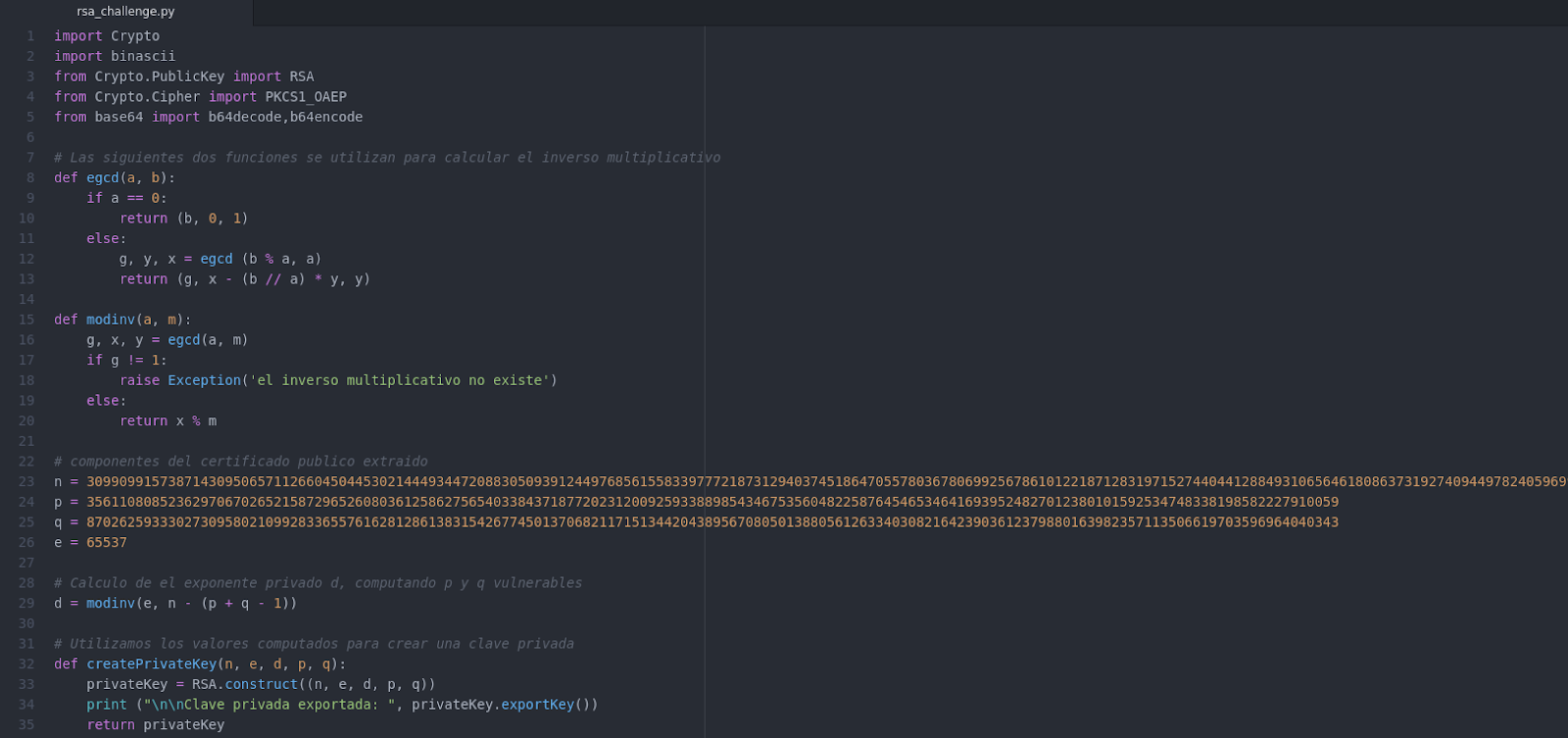
Fig 2. Código para generar la clave privada
En la Fig. 3 podemos ver el resultado que genera en el terminal

Fig 3. Clave privada en formato PEM
Con la clave privada obtenida, ya podemos descifrar el mensaje obtenido sniffeando la red. Para ello utilizamos la clase PKCS1_OAEP de la librería de pycrypto nuevamente.
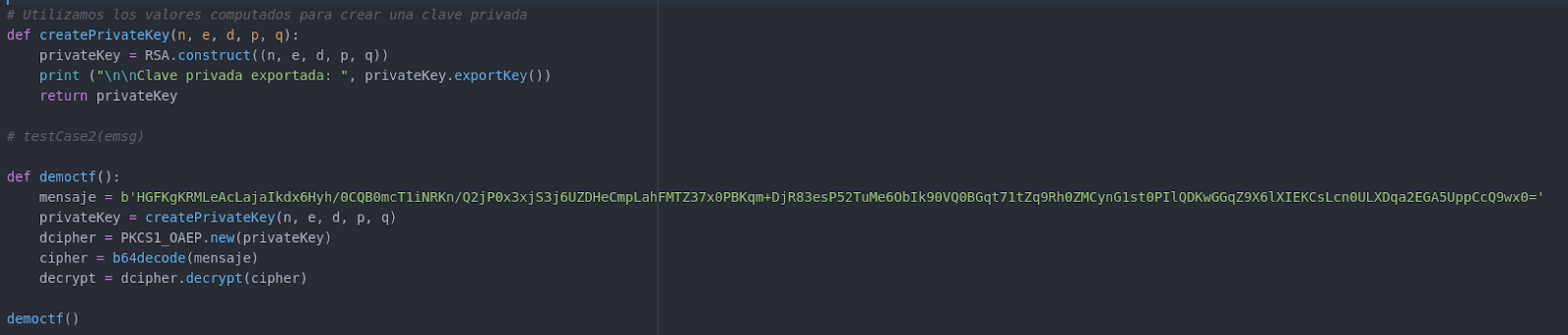
Fig 4. Código para descifrar el mensaje secreto
Finalmente, al ejecutar el método democtf(), obtenemos:
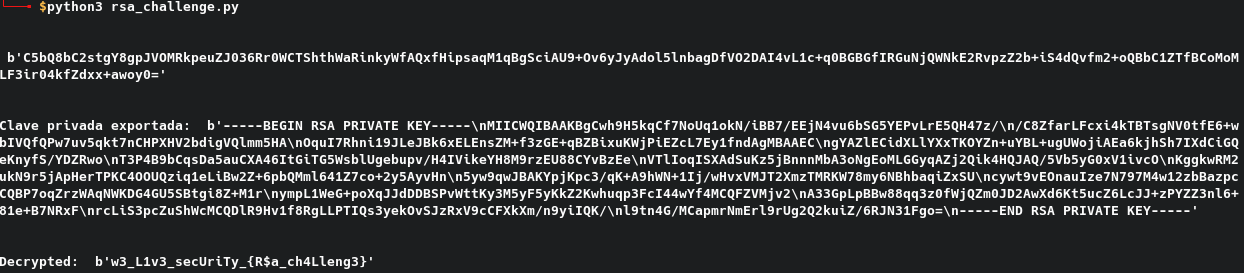
Fig 5. Mensaje descifrado
el flag del desafío es: w3_L1v3_secUriTy_{R$a_ch4Lleng3}
Agradecemos que hayan participado y esperamos que hayan disfrutado de este desafío.





