Embora existam métodos para criptografar informações há mais de mil anos, a criptografia como disciplina matemática ganhou grande importância a partir do século XX, quando a pesquisa formal começou a ser realizada sobre os diferentes métodos, algoritmos e sua segurança. Com o passar dos anos e os consequentes avanços na computação, o foco já não é apenas proteger as comunicações, mas também os dados e, particularmente, os dados que devem ser usados constantemente.
Como as operações de criptografia e descriptografia frequentemente consomem recursos computacionais ou são pontos de falha para vazamento de informações, surgiu uma linha de pesquisa chamada criptografia homomórfica.
O principal objetivo deste tipo de codificação é poder realizar operações diretamente sobre os dados criptografados, sem necessidade de descriptografá-los previamente ou de dispor da chave com que foram criptografados. Desta forma é possível reduzir o número de vezes que os dados devem ser descriptografados, com a vantagem de reduzir a probabilidade dos dados poderem ser roubados e, ao mesmo tempo, ao não ser necessário descriptografar os dados para utilizá-los, pode-se ter um controle muito mais rigoroso sobre a disponibilidade da informação, garantindo a sua integridade e confidencialidade.
Este tipo de esquema de criptografia foi proposto pela primeira vez em 1978 por Ronald Rivest, Adleman e Dertouzos (Rivest e Adleman publicaram o famoso algoritmo RSA juntamente com Shamir). No entanto, isso não significou uma etapa de prosperidade para essas pesquisadores, uma vez que a viabilidade teórica para a criação de um esquema de criptografia totalmente homomórfico - que permite qualquer tipo de operação - não foi demonstrado. Foi Craig Gentry quem, em 2009, lançou as bases teóricas para a construção de tal esquema para que pudesse ser ao mesmo tempo seguro e eficiente, dando origem a múltiplas pesquisas e avanços que continuam até hoje.
A ideia básica do funcionamento destes sistemas baseia-se no conceito de homomorfismo matemático, que estabelece o seguinte:
Considerando dois grupos (A, .) e (B, *) e uma função F: A->B que toma elementos do conjunto A e retorna elementos do conjunto B. F é um homomorfismo se e somente se F(x . y) = F(x)*F(y) para qualquer par de elementos "x" e "y" pertencentes ao conjunto A.
Então, ao mapear este conceito com criptografia, o conjunto A pode ser interpretado como um texto simples, o conjunto B como o texto criptografado, '.' como as operações que podem ser executadas sobre o texto simples, '*' como as operações que podem ser realizadas nos dados criptografados, e finalmente F como a função de criptografia.
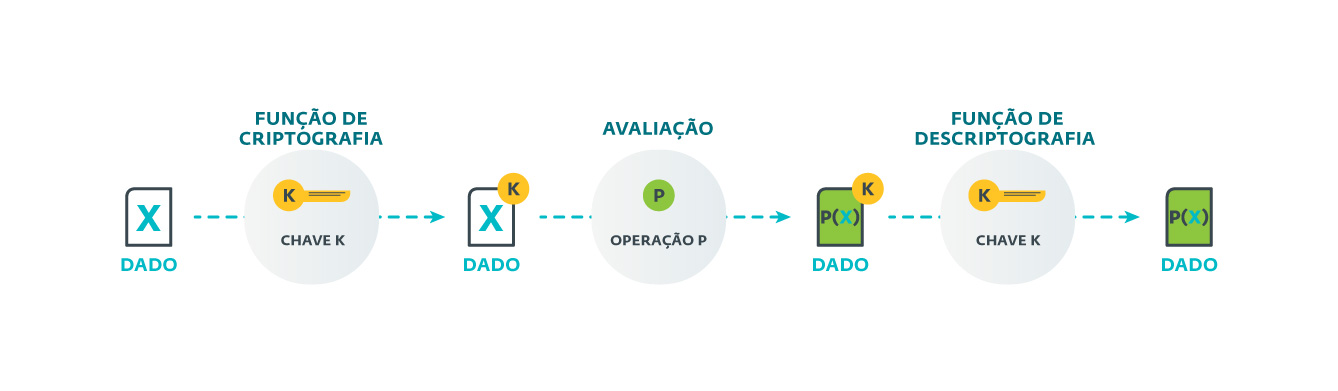
Imagem 1. Esquema geral da dinâmica de funcionamento da criptografia homomórfica.
Um detalhe impressionante é que os algoritmos de criptografia mais comuns são normalmente concebidos para não ter propriedades de homomorfismo para que os dados criptografados não tenham uma estrutura relacionada com os dados originais. No caso da criptografia homomórfica, embora seja segura, dependendo do algoritmo em questão e de sua implementação particular, pode se deparar com um ataque que explore essa característica.
O interessante é que, além de ser aplicada em vários ambientes, muitas das vantagens oferecidas por este tipo de esquema criptográfico cobrem as necessidades dos modelos de negócio atuais. Portanto, seu uso pode ser benéfico na gestão de dados médicos, sistemas de votação eletrônica, sistemas de computação forense e especialmente para serviços encadeados ou centrados na nuvem; o que pode ser de grande interesse atualmente, uma vez que com o surgimento da "transformação digital" o número de empresas e indivíduos que utilizam serviços em nuvem está crescendo.
O desafio neste tipo de serviço é o elevado volume de dados e que estes devem ser transmitidos criptografados para, em seguida, serem descriptografados - permanecendo neste ponto vulnerável - durante o processamento num servidor externo, sobre o qual normalmente não há muito controle e, consequentemente, caso seja comprometido, poderá resultar na perda da confidencialidade desses dados. É por isso que este tipo de situação é ideal para o uso de criptografia homomórfica em que, podendo trabalhar com dados criptografados, surge a possibilidade de que outros possam ter acesso a eles, usando-os sem comprometer sua integridade ou confidencialidade.
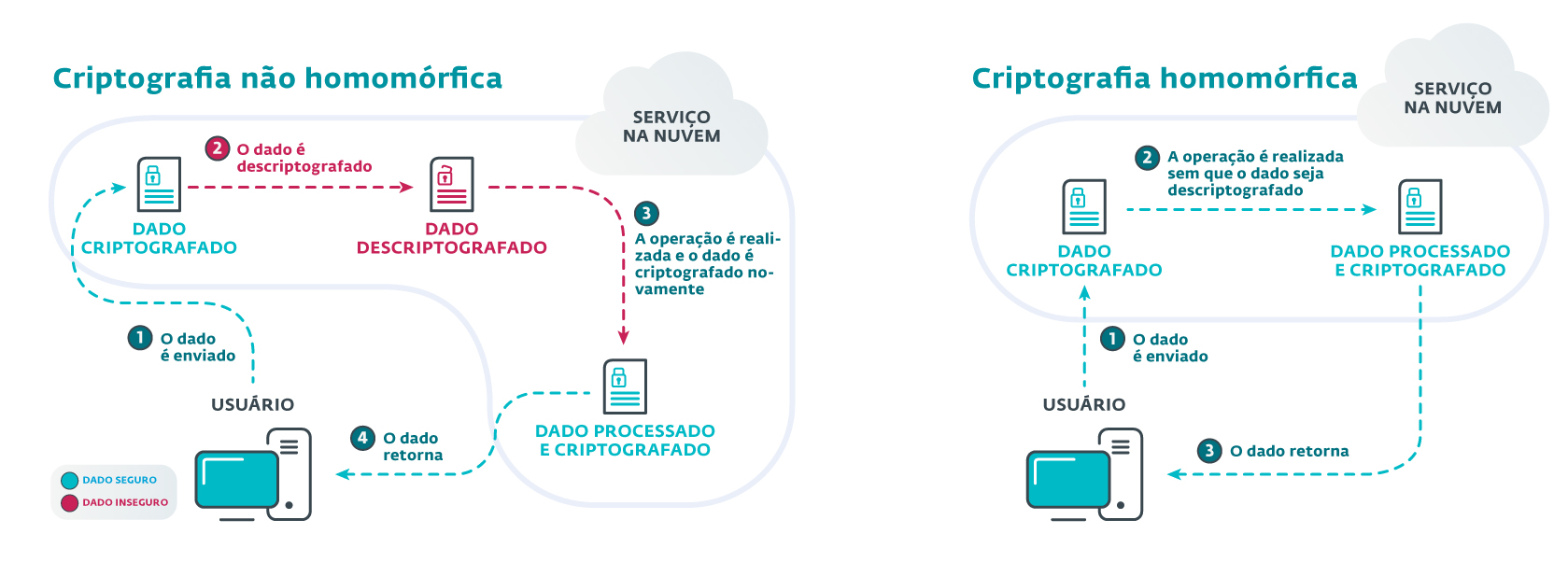
Imagem 2. Esquema comparativo entre criptografia não homomórfica e homomórfica.
Atualmente, os sistemas de criptografia homomórfica são classificados em categorias de acordo com as propriedades e a variedade de operações que podem ser realizadas em dados criptografados. Estes são: Somewhat Homomorphic, Levelled Homomorphic e Fully Homomorphic.
As operações são representadas por circuitos de comportas lógicas e, dependendo da categoria, estes circuitos podem ser maiores ou ter uma maior ou menor variedade de operações. Os sistemas Fully Homomorphic (FHC) permitem que qualquer tipo de operação seja realizada nos dados, embora eles ainda tenham limitações importantes quando operações muito longas e complexas são utilizadas devido à sobrecarga de computação necessária para usá-los. As outras categorias têm melhor desempenho, mas com uma variedade mais limitada de operações. Portanto, cada categoria tem suas vantagens e desvantagens e é importante avaliar em que tipo de cenário elas serão aplicadas.
Embora a criptografia homomórfica seja uma área muito promissora e já existam implementações de diferentes esquemas de criptografia, estes ainda apresentam muitas questões a serem resolvidas e estão em contínuo desenvolvimento e pesquisa; o que demonstra a crescente necessidade de sistemas funcionais e seguros para lidar com informações sensíveis. Atualmente, muitas empresas estão buscando promover a definição de padrões através de diversas iniciativas como a homomorphicencryption.org, que é apoiada pela Microsoft, Intel, IBM e muitas outras empresas e grandes órgãos governamentais. Dada a recente explosão no uso de serviços em nuvem, espera-se que estes se tornem ainda mais relevantes nos próximos anos, especialmente quando os diferentes algoritmos se tornarem padrões e forem adotados por várias organizações.





